
史密斯圆图-初诞
作者:N0AX 翻译:BH4SRC
传输线的工作原理和方法是神秘且难以理解的,众生膜拜的史密斯圆图就是能破解它的宝物么?不,显然不是。不过史密斯圆图是一扇能够观测传输线内部工作状况的窗口,利用它我们可以更好地理解传输线的工作机制。
背景知识
QST杂志和维基百科网站关于史密斯圆图的介绍,要比这个栏目的文章讨论的更深。你可以先读读这些文章,也可以把它们作为学习这个栏目文章的参考文献。
在讨论史密斯圆图前,让我们先回顾下基础知识。所有阻抗由两个分量构成,即电阻和电抗。作图来看的话,这两个分量可以用一对90°垂直的轴来表示,如图一。横轴表示电阻,原点向右为正,原点向左为负。竖轴表示电抗,原点向上为正(代表感抗),原点向下为负(代表容抗)。

图中任一点(Z)所能表示的阻抗值都是基于特定电阻值和电抗值。这两个值就是阻抗的直角坐标系表达法,记住这一点。
再来看看传输线,当射频电压波和电流波在传输线中遇到不同于馈线特性阻抗值Z0的阻抗时,射频能量的一部分就会沿着传输线返回,构成反射波。反射波的电压和电流相位与入射波的电压和电流的相位不同,相位差值由造成反射的阻抗值决定。
电压和电流的入射波和反射波在传输线上的每个点都混合,混合后的电压和电流相位,与入射波和反射波的电压和电流的相位都不同。就好像传输线上同样的能量被分给了构成同样相位关系电阻值和电抗值。如果你在那个点的位置把传输线切断,并在切口位置接上一个有等效阻抗值的真实元件替代后面的一段馈线,这将对剩下的这一段传输线中的射频波没有任何改变。 射频波的电压和电流随着传输线的长度变化而变化,这是由于射频波的交流特性造成的。这也就导致了入射波和反射波的电流和电压以及等效阻抗值会不同。比如,某点的等效阻抗值是5Ω电阻和+20Ω的电抗,沿着传输线上更远的某点等效值可能是20Ω电阻和-5Ω的电抗。这就是说图中具有某个电阻和电抗值的点也会在传输线中来回移动,半个波长后又回到开始时的电压和电流值。
构建史密斯圆图
说这些和史密斯圆图有什么关系呢?描述阻抗值点在直角坐标系中运动的公式如下: Z=Z0[(ZL +jZ0 × tan(β1))/(Z0 +jZL × tan(β1))] 使用公式在图中所表示路径很不方便(β1表示的是在传输线中的电气位置)。可是史密斯发现,如果你以某种方式扭曲直角坐标系图的话(称为映射),路径就变成了圆!
如何实现这一神奇的映射呢?假想一下你就站在直角坐标系的原点位置,电阻的正轴部分在你得面前,而负轴部分在你身后。电抗的正轴从你的脚下向上延伸,而负轴则笔直向下。所有的轴都伸向无穷远处。
此刻想象你抬起头来,把电抗正轴向下弯曲到你面前(发出你喜欢的任何噪声)形成一个半圆,这时,电抗正轴的无穷远点和电阻正轴的无穷远点重合。再次弯曲电抗的负轴,只是要把它向上弯曲。这时电阻的负轴还在你身后笔直的伸向远处,这一过程可以用图二来概述。
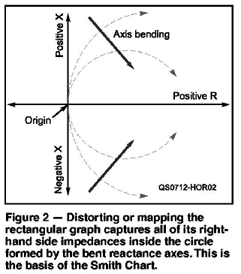
走到一旁,看看你得手工作品吧。你创造出了一个被阻抗轴分为两半的圆。原来三个半轴上的无穷远点在图的右边重复在一起。原来在直角坐标系图中位于右半边的点,此刻都在圆内或者圆的边界上。而原来直角坐标系中左边的点都在圆的外部。什么都没有被遗漏,只是被压扁了而已。
史密斯圆图(见图三)只包含圆上和圆内部分的值,而忽略了圆外的一切值,这是因为圆外这些点的电阻值都是负值。这些点也是位于直角坐标系中左半边的位置,而在传输线中出现不了电阻值为负值的情况。

史密斯圆图中圆和圆弧揭示了直角坐标系中直线被映射后结果。具有恒定电阻值的线,在直角坐标系中时曾经是一条条垂直直线,这些线上所有点都有相同的电阻值。映射后,这些直线变成了常电阻值圆,并在史密斯圆图的最右端交于一点。这也说得通,因为这些线曾经都是指向无穷远处,现在则指向了史密斯圆图的右边的一个点。具有相同电抗值的水平线,现在则被弯曲为常电抗值圆弧。圆弧的一个端点在外圆上(直角坐标系中垂直的电抗轴),另一个端点则位于无穷点。这一扭曲让曾经是直线的阻抗值路径,在史密斯圆图中则变成了一个圆。
画一个圆
你可以自己标示,来看看这个圆是如何实现的。你需要一台可以显示电阻值(R)和电抗值(X)的天线分析仪,能否显示电抗值的正负号不做要求。
剪一段10MHz二分之一波长电气长度的传输线,自由空间中10MHz二分之一波长的长度是15米。如果传输线的速度因子是0.66,那么你需要的传输线长度就是9.9米(15 × 0.66)。在传输线的一头接上一个同轴馈线接头,再将传输线另一头短路并用天线分析仪测量X值为0(或者最小时)的最低频率值。这就是传输线二分之一波长长时的频率值,记下这个频率值。用150Ω电阻代替短路线,此时天线分析仪的读数应该是3:1,阻抗值是R=150Ω,X=0。在直角坐标系图中,这个点是在水平的电阻轴线上150Ω的位置。
打印一张史密斯圆图,如果你在图中寻找R=150Ω,X=0这个点,你会发现它就躲在这张被压扁了到处都是圆圈的图的右边,这样的图用起来易用性很差。史密斯用归一化方法避免了大数字的问题,原理就是用直角坐标系中的阻抗值除以传输线的特性阻抗值,Z0 。归一化就是把每个点的值用它们和Z0的比值来替代实际值,在本例中就是除以50Ω。因此,把横轴的150Ω除以50Ω,得到3.0 。这下就容易多了。从这开始,你在史密斯圆图上标识的每一个值,就用表上的读数除以50Ω后得到的数字即可。
以0.5MHz为步进,增加表上的频率,在史密斯圆图上记录R和X值。由于天线分析仪可能不会显示电抗的正负号,假设你增加频率后,电抗值变为负数(容性)。当电抗值再次为0时暂停,此时电阻值为50/3=16.7Ω,在史密斯圆图水平轴上标识下16.7/50=0.33这个点。这时的频率就是长度为四分之三波长长度的频率。当你在标识点时,SWR值并没有改变。
你标识的点最终会形成一个如图三所示的半圆,半圆最低点的值是R=0.6Ω、X=-0.8Ω,也就是未归一化的阻抗值30-j40Ω。继续增加频率直至回到横轴上开始标识时的3.0这个点。此时传输线是全波长,天线分析仪上的频率此时应该是开始时频率的2倍。所有点构成的这个圆,被称为SWR常值圆,因为这个圆上的所有点都具有相同的SWR值。
如果你想知道为什么史密斯圆图这么有用,就把这些归一化后的值在等比例、横轴0到5Ω,纵轴-5到5Ω的直角坐标系上标识下就知道了。你会更喜欢用哪种图来标识呢?
本文仅是开始,下期我们会继续探索史密斯圆图。本文中使用的天线分析仪别拆下,找找本文开头所提到的参考文献看看。希望史密斯圆图从现在开始,对你能够有更多一些意义。